Pontecorvo–Maki–Nakagawa–Sakata matrix

Flavour in particle physics
Flavour quantum numbers:

Related quantum numbers:

Combinations:

Flavour mixing

In particle physics, the Pontecorvo–Maki–Nakagawa–Sakata matrix (PMNS matrix), Maki–Nakagawa–Sakata matrix (MNS matrix), lepton mixing matrix, or neutrino mixing matrix, is a unitary matrix[note 1] which contains information on the mismatch of quantum states of leptons when they propagate freely and when they take part in the weak interactions. It is important in the understanding of neutrino oscillations. This matrix was introduced in 1962 by Ziro Maki, Masami Nakagawa and Shoichi Sakata,[1] to explain the neutrino oscillations predicted by Bruno Pontecorvo.[2][3]

Contents

The matrix

For three generations of leptons, the matrix can be written as:

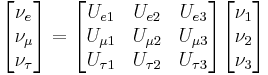\begin{bmatrix} {\nu_e} \\ {\nu_\mu} \\ {\nu_\tau} \end{bmatrix} = \begin{bmatrix} U_{e 1} & U_{e 2} & U_{e 3} \\ U_{\mu 1} & U_{\mu 2} & U_{\mu 3} \\ U_{\tau 1} & U_{\tau 2} & U_{\tau 3} \end{bmatrix} \begin{bmatrix} \nu_1 \\ \nu_2 \\ \nu_3 \end{bmatrix} \ .

On the left are the neutrino fields participating in the weak interaction, and on the right is the PMNS matrix along with a vector of the neutrino fields diagonalizing the neutrino mass matrix. The PMNS matrix describes the probability of a neutrino of given flavor α to be found in mass eigenstate i. These probabilities are proportional to |Uαi|2.

Various parametrizations of this matrix exist,[4] however due to the difficulties of detecting neutrinos, it is much more difficult to determine the individual coefficients than in the equivalent matrix for the quarks (the CKM matrix). The matrix is most commonly parameterized by three mixing angles (Θ12, Θ23 and Θ13) and a single phase. Experimentally, the mixing angles were established to be approximately Θ12=45 degrees, Θ23=34 degrees, and Θ13<4 degrees.

As a starting point, one recent particle physics course[5] provided the following estimated values for the matrix (assuming the mixing angle Θ13=0, which is in good agreement with the experiment, and therefore no imaginary parameters in the matrix):

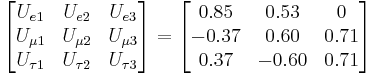\begin{bmatrix} U_{e 1} & U_{e 2} & U_{e 3} \\ U_{\mu 1} & U_{\mu 2} & U_{\mu 3} \\ U_{\tau 1} & U_{\tau 2} & U_{\tau 3} \end{bmatrix} = \begin{bmatrix} 0.85 & 0.53 & 0 \\ -0.37 & 0.60 & 0.71 \\ 0.37 & -0.60 & 0.71 \end{bmatrix} \ .

See also

Notes

  1. ^ The PMNS matrix is not unitary in the seesaw model

References

  1. ^ Z. Maki, M. Nakagawa, and S. Sakata (1962). "Remarks on the Unified Model of Elementary Particles". Progress of Theoretical Physics 28: 870. Bibcode 1962PThPh..28..870M. doi:10.1143/PTP.28.870. 
  2. ^ B. Pontecorvo (1957). "Mesonium and anti-mesonium". Zh. Eksp. Teor. Fiz. 33: 549–551.  reproduced and translated in Sov. Phys. JETP 6: 429. 1957. 
  3. ^ B. Pontecorvo (1967). "Neutrino Experiments and the Problem of Conservation of Leptonic Charge". Zh. Eksp. Teor. Fiz. 53: 1717.  reproduced and translated in Sov. Phys. JETP 26: 984. 1968. Bibcode 1968JETP...26..984P. 
  4. ^ J.W.F. Valle (2006). "Neutrino physics overview". Journal of Physics: Conference Series 53: 473. arXiv:hep-ph/0608101. doi:10.1088/1742-6596/53/1/031. 
  5. ^ http://www.hep.phy.cam.ac.uk/~thomson/partIIIparticles/handouts/Handout11_2010.pdf